Shepard.cl File Reference

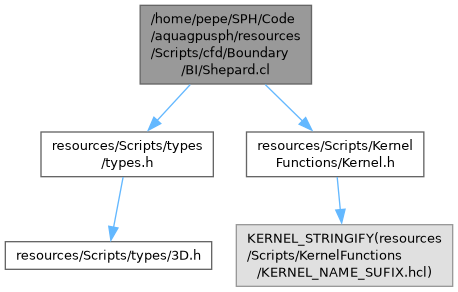
Boundary integral term computation. (See Aqua::CalcServer::Boundary::DeLeffe for details) More...

#include "resources/Scripts/types/types.h"
#include "resources/Scripts/KernelFunctions/Kernel.h"

Include dependency graph for Shepard.cl:

Macros
#define	_SHEPARD_   shepard[i]

Functions
__kernel void	compute (const __global int *imove, const __global vec *r, const __global vec *normal, const __global vec *tangent, const __global vec *binormal, const __global float *m, __global float *shepard, const __global uint *icell, const __global uint *ihoc, uint N, uivec4 n_cells)
	Shepard factor computation.
__kernel void	apply (const __global int *imove, const __global float *shepard, __global vec *grad_p, __global vec *lap_u, __global float *div_u, uint N, float cs)
	Renormalize the differential operators.

Detailed Description

Boundary integral term computation. (See Aqua::CalcServer::Boundary::DeLeffe for details)

Macro Definition Documentation

_SHEPARD_

#define _SHEPARD_   shepard[i]

Function Documentation

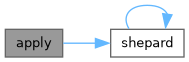
apply()

__kernel void apply	(	const __global int *	imove,
		const __global float *	shepard,
		__global vec *	grad_p,
		__global vec *	lap_u,
		__global float *	div_u,
		uint	N,
		float	cs
	)

Renormalize the differential operators.

The main drawback of the boundary integrals formulation is the requirement of the renormalization of the computed differentiqal operators, which is destroying several conservation properties.

Parameters

imove	Moving flags. imove > 0 for regular fluid particles. imove = 0 for sensors. imove < 0 for boundary elements/particles.
shepard	Shepard term \( \gamma(\mathbf{x}) = \int_{\Omega} W(\mathbf{y} - \mathbf{x}) \mathrm{d}\mathbf{x} \).
grad_p	Pressure gradient \( \frac{\nabla p}{rho} \).
lap_u	Velocity laplacian \( \frac{\Delta \mathbf{u}}{rho} \).
div_u	Velocity divergence \( \rho \nabla \cdot \mathbf{u} \).
N	Total number of particles and boundary elements.
cs	Speed of sound \( c_s \).

See also

Boundary/BI/Interactions.cl

Here is the call graph for this function:

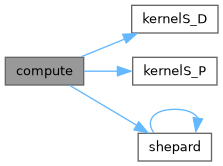
compute()

__kernel void compute	(	const __global int *	imove,
		const __global vec *	r,
		const __global vec *	normal,
		const __global vec *	tangent,
		const __global vec *	binormal,
		const __global float *	m,
		__global float *	shepard,
		const __global uint *	icell,
		const __global uint *	ihoc,
		uint	N,
		uivec4	n_cells
	)

Shepard factor computation.

\[ \gamma(\mathbf{x}) = \int_{\Omega} W(\mathbf{y} - \mathbf{x}) \mathrm{d}\mathbf{y} \]

The shepard renormalization factor is applied for several purposes:

• To interpolate values
• To recover the consistency with the Boundary Integrals formulation
• Debugging

In the shepard factor computation the fluid extension particles are not taken into account.

Parameters

imove	Moving flags. imove > 0 for regular fluid particles. imove = 0 for sensors. imove < 0 for boundary elements/particles.
r	Position \( \mathbf{r} \).
normal	Normal \( \mathbf{n} \).
tangent	Tangent \( \mathbf{t} \).
binormal	Binormal \( \mathbf{b} \).
m	Area of the boundary element \( s \).
shepard	Shepard term \( \gamma(\mathbf{x}) = \int_{\Omega} W(\mathbf{y} - \mathbf{x}) \mathrm{d}\mathbf{y} \).
icell	Cell where each particle is located.
ihoc	Head of chain for each cell (first particle found).
N	Number of particles.
n_cells	Number of cells in each direction

Here is the call graph for this function: